Vài quy luật toán học đáng kinh ngạc của Lạc Thư

Chia sẻ Facebook

Hà Đồ, Lạc Thư và Bát Quái là ba họa đồ được truyền lại từ thời xa xưa, có nguồn gốc từ các bộ tộc phía Nam sông Dương Tử cổ đại (là nơi phát tích của người Việt cổ). Mỗi họa đồ được truyền tụng, phát triển, và sử dụng với nhiều mục đích khác nhau, kể cả trong toán học.

Theo truyền thuyết cổ xưa, trên sông Hoàng Hà đã từng xuất hiện một con long mã trên mình có vẽ Hà Đồ. Còn trên sông Lạc Thủy xuất hiện con thần quy, trên lưng có vẽ Lạc Thư. Phục Hy căn cứ vào Hà Đồ để suy diễn ra Tiên thiên Bát quái, còn Chu Văn Vương lại căn cứ vào Lạc Thư để suy diễn ra Hậu thiên Bát quái. Theo đó, những đồ hình này hàm chứa nhận thức của cổ nhân về vũ trụ.

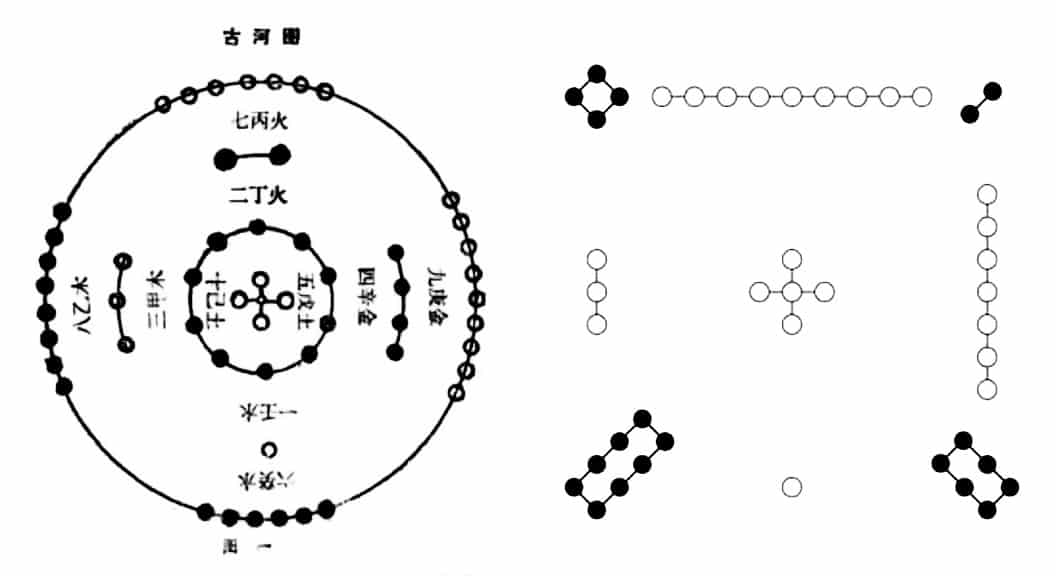
Hà Đồ và Lạc Thư.

Ngày nay, những người đam mê Kinh Dịch, thuật số, lý học vẫn luôn xoay quanh những đồ hình ấy để nghiên cứu. Dưới đây là một vài quy luật toán học đáng kinh ngạc của Lạc Thư.

Lạc Thư.

Lạc Thư nhìn thì thấy là một đồ hình hình vuông, gọi là “phương đồ”. Có ba hàng, gọi là hoành, có ba cột, gọi là tung. Người ta cũng gọi Lạc Thư là Tung Hoành Đồ. Chúng ta để ý số lượng các dấu chấm trong Lạc Thư này và thay thế chúng bằng các chữ số để biểu thị. Như vậy ta được một ma trận 3×3 như sau:

Ma trận Lạc Thư.

Sự sắp xếp của các chữ số trên Lạc Thư, nhìn thì thấy rất đơn giản, chỉ có 1, 2, 3, 4, 5, 6, 7, 8, 9, chỉ có 9 chữ số đó. Nhưng các chữ số đơn giản, chiểu theo cách sắp xếp đặc biệt của nó, kết quả lại sản sinh ra các quy luật chữ số không đơn giản.

Quy luật thứ nhất

Hàng trên là 4, 9, 2, cộng lại là 15, hàng giữa là 3, 5, 7, cộng lại là 15, hàng dưới là 8, 1, 6, cộng lại là 15.

4+9+2=15 3+5+7=15 8+1+6=15

Cột trái là 4, 3, 8, cộng lại là 15, cột giữa là 9, 5, 1, cộng lại là 15, cột phải là 2, 7, 6, cộng lại là 15.

4+3+8=15 9+5+1=15 2+7+6=15

Đường chéo chính là 4, 5, 6, cộng lại là 15, đường chéo phụ là 2, 5, 8, cộng lại là 15.

4+5+6=15 2+5+8=15

Ngang dọc và đường chéo, các phương hướng khác nhau, ba số cộng lại, đều là 15. Do đó người ta cũng gọi Lạc Thư là huyền phương (hình vuông huyền diệu).

Quy luật thứ hai

Phương, rất dễ khiến người ta nghĩ đến bình phương. Bình phương, cách dùng sơ khai lúc ban đầu là để tính toán diện tích, diện tích hình vuông bằng bình phương độ dài cạnh. Khi chúng ta dùng bình phương để tính toán Lạc Thư, thì xuất hiện nhiều quy luật chữ số hơn.

Hàng trên là 4, 9, 2, tổng bình phương là 101; hàng dưới là 8, 1, 6, tổng bình phương là 101.

4^2+9^2+2^2=101 8^2+1^2+6^2=101

Cột trái là 4, 3, 8, tổng bình phương là 89; cột phải là 2, 7, 6, tổng bình phương là 89.

4^2+3^2+8^2=89 2^2+7^2+6^2=89

Quy luật thứ ba

Tổng hợp vận dụng hai quy luật ở trên, còn có một số cách tính thú vị sau:

Lấy hàng trên và hàng dưới, chiểu theo cách kết hợp vị trí từ trái qua phải mà tổng hợp ra số có hai chữ số. Hàng trên được 49, 92, 24, tổng bình phương của chúng là 11441. Hàng dưới được ba số là 81, 16, 68, tổng bình phương cũng là 11441.

49^2+92^2+24^2=11441 81^2+16^2+68^2=11441

Lấy cột trái và cột phải, chiểu theo cách tổ hợp tương tự như trên. Cột trái được 43, 38, 84, tổng bình phương là 10349, cột phải được 27, 76, 62, tổng bình phương là 10349.

43^2+38^2+84^2=10349 27^2+76^2+62^2=10349

Lấy hàng trên và hàng dưới, chiểu theo cách tổ hợp từ trái sang phải mà tổ hợp thành số có ba chữ số. Hàng trên được 492, 924, 249. Tổng bình phương là 1157841. Hàng dưới được 816, 168, 681, tổng bình phương là 1157841.

492^2+924^2+249^2=1157841 816^2+168^2+681^2=1157841

Lấy cột trái và cột phải, chiểu theo cách tổ hợp từ trên xuống dưới mà tổ hợp thành số có ba chữ số, cột trái được 438, 384, 843, tổng bình phương là 1049949. Cột phải được 276, 762, 627, tổng bình phương là 1049949.

438^2+384^2+843^2=1049949 276^2+762^2+627^2=1049949

Nếu lấy số có bốn chữ số, thì cũng ra được quy luật tương tự.

Quy luật thứ tư

Ở trên nói về các cách tính bình phương, và không dùng đến hàng giữa và cột giữa, nếu dùng để tính thì cũng có những quy luật rất thú vị.

Lấy hàng trên và hàng giữa, tổ hợp lần lượt thành các số có hai chữ số, thì được 43, 95, 27; lấy hàng dưới và hàng giữa, tổ hợp lần lượt thành các số có hai chữ số, thì được 83, 15, 67.

43^2+95^2+27^2=11603 83^2+15^2+67^2=11603

Lấy cột trái và cột giữa, chiểu theo cách tổ hợp lần lượt để hình thành các số có hai chữ số thì được 49, 35, 81. Lấy cột phải, cột giữa, tổ hợp được các số 29, 75, 61.

49^2+35^2+81^2=10187 29^2+75^2+61^2=10181

Quy luật thứ năm

Nếu dùng hết các số của các hàng các cột của Lạc Thư, cũng được một quy luật toán học kỳ diệu:

Lấy ba hàng, theo thứ tự xuôi và ngược mà tổ hợp thành các số có ba chữ số:

492^2+357^2+816^2=1035369 294^2+753^2+618^2=1035369

Lấy ba cột, cũng theo thứ tự xuôi ngược mà tổng hợp thành các số có ba chữ số:

438^2+951^2+276^2=1172421 834^2+159^2+672^2=1172421

Ở đây chỉ đưa ra năm quy luật, chỉ là phần nông nhất của Lạc Thư, những điều này chỉ thuần túy là toán học, là tính toán chữ số. Suy nghĩ cẩn thận một chút, đi sâu tìm hiểu một chút nữa, chúng ta nhất định sẽ cảm động sâu sắc đối với Lạc Thư. Biểu đồ số đơn giản như vậy mà lại có thể ẩn tàng nhiều quy luật đến thế.

Trong con mắt của người hiện đại, Lạc Thư rất đơn giản, một đứa trẻ con học toán rồi cũng có thể làm ra. Đa số người trưởng thành không có hứng thú gì với Lạc Thư. Nhưng vào thời cổ đại, nơi Trung Hoa huyền bí ấy vẫn luôn có những người trí huệ cao đi nghiên cứu sự thâm sâu huyền bí của Lạc Thư. Nếu kết hợp Hà Đồ với Lạc Thư thì sẽ thấy ẩn tàng chữ Vạn của Phật gia và Thái Cực của Đạo gia. (Xem bài cũ tại đây )

(Ảnh: Nattawut Jaroenchai & Serg Zastavkin, Shutterstock)

Trong mắt của cổ nhân, Lạc Thư là đồ hình sao thời thượng cổ, có ảnh hưởng huyền diệu thâm sâu đối với thiên văn địa lý. Lạc Thư là văn hóa tiền sử, biểu đạt nhận thức của con người thời văn minh tiền sử đối với quy luật vận hành của hệ Ngân Hà. Văn hóa thuật số qua các thời đại, không cái nào là không vận dụng sự thâm sâu huyền diệu của Lạc Thư.

Thuật số mạn đàm: Quy luật của các chữ số trên Lạc Thư

Đăng trên ChanhKien.org

Tác giả: Cửu Số

Mời nghe radio :

Chia sẻ Facebook